El algebra es una rama de las matematicas que se ocupa de estudiar las propiedades generales de las operaciones aritmeticas y lo números para generar procedimientos que puedan globalizarse para todos los casos analogos. esta rama se caracteriza por hacer implicitas las incognitas dentro de la misma operación; ecuación algebraica.
PENSAMIENTO ALGEBRAICO Y NUMERICO
QUIE ES EL PADRE DEL ALGEBRA
Diofanto de Alejandría No se sabe nada de la patria de este matemático griego y muy poco referente a su vida. Perteneció a la escuela alejandrina, nació hacia el 250 y murió a los ochenta y cuatro años

Temario de Pensamiento Algebraico
TEMARIO DE PENSAMIENTO ALGEBRAICO
VARIACIONES NUMERICAS
1.1. VARIACIONES
1.1.1. REGLA DE TRES EN CONTEXTO
1.1.2. NOCION DE VARIACION A PARTIR DE UN COMPORTAMIENTO DE CASOS CONTEXTUALIZADOS.
1.1.3. VARIACION PROPORCIONAL ENTRE DOS CANTIDADES
1.1.4. CONSTANTE DE PROPORCIONALIDAD EN TABLAS, GRAFICAS Y DE FORMA ANALITICA
1.1.5. TABULACION Y VARIACION NUMERICA CONTEXTUALIZADA
1.1.6. TABULACION Y VARIACION EN PLANO CARTESIANO
UNIDAD DOS
FUNCIONES Y MODELOS MATEMATICOS
2.1. FUNCION CON MODELO MATEMATICO
2.1.1. NOCION DE FUNCION
2.1.2. MODELOS DE FUNCIONES EN CONTEXTO: LINEAL, CONSTANTE, CUADRATICA, POLINOMICA, EXPONENCIAL Y LOGARITMICA
2.1.3. TABULACION Y GRAFICACION DE FUNCIONES
2.1.4. CONTINUIDAD Y DISCONTINUIDAD DE UNA FUNCION DE FORMA GRAFICA
2.1.5. ANALISIS DE FUNCIONES INTERSECCION CON LOS EJES DE LAS ABSISAS (LAS RAICES) Y LAS ORDENADAS, PUNTO DE INFLEXION, MAXIMOS Y MINIMOS.
UNIDAD TRES
FUNCIONES Y ECUACIONES LINEALES EN CONTEXTO
3.1.1. LA ECUACION LINEAL EMANADA DE LA FUNCION EN CONTEXTO
3.1.2. LOS SISTEMAS DE ECUACIONES COMO FUNCIONES EN CONTEXTO: METODO GRAFICO Y ANALITICO.
UNIDAD CUATRO
FUNCIONES Y ECUACIONES CUADRATICAS EN CONTEXTO
4.1.1. ECUACIONES CUADRATICAS EMANADAS DE LA FUNCION EN CONTEXTO
4.1.2 LA ECUACION CUADRATICA Y SUS METODOS DE SOLUCION: METODO GRAFICO Y ANALITICO

Proporcionalidad: directa e inversa |
Para comprender el concepto de proporcionalidad, directa o inversa, debemos comenzar por comprender el concepto de razón.
Razón y proporción numérica
Razón entre dos números
Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos.
Entonces:
|
Razón entre dos números a y b es el cociente entre |
|
|
Por ejemplo, la razón entre 10 y 2 es 5, ya que
|
|
Y la razón entre los números 0,15 y 0,3 es
|
|
Proporción numérica
Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver como se comportan entre ellas, estaremos hablando de una proporción numérica.
Entonces:
| Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que entre c y d. | |
|
Es decir
|
|
| Se lee “a es a b como c es a d” | |
Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.
|
Es decir
|
|
| En la proporción | hay cuatro términos; a y d se llaman extremos, c y b se llaman medios. |
|
La propiedad fundamental de las proporciones es: en toda proporción, el producto de los extremos es igual al de los medios. |
|
Así, en la proporción anterior
|
se cumple que el producto de los extremos nos da 2 x 20 = 40 y el producto de los medios nos da 5 x 8 = 40
|
|
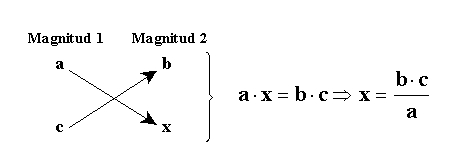
Comprendido el concepto de proporción como una relación entre números o magnitudes, ahora veremos que esa relación puede darse en dos sentidos:
Las dos magnitudes pueden subir o bajar (aumentar o disminuir) o bien si una de las magnitudes sube la otra bajo y viceversa.
Si ocurre, como en el primer caso, que las dos magnitudes que se comparan o relacionan pueden subir o bajar en igual cantidad, hablaremos de Magnitudes directamente proporcionales.
Si ocurre como en el segundo caso, en que si una magnitud sube la otra baja en la misma cantidad, hablaremos de Magnitudes inversamente proporcionales.
MAGNITUDES DIRECTAMENTE PROPORCIONALES
|
Si dos magnitudes son tales que a doble, triple... cantidad de la primera corresponde doble, triple... cantidad de la segunda, entonces se dice que esas magnitudes son directamente proporcionales. |
Ejemplo
Un saco de papas pesa 20 kg. ¿Cuánto pesan 2 sacos?
Un cargamento de papas pesa 520 kg ¿Cuántos sacos de 20 kg se podrán hacer?
|
Número de sacos |
1 |
2 |
3 |
... |
26 |
... |
|
Peso en kg |
20 |
40 |
60 |
... |
520 |
... |
Para pasar de la 1ª fila a la 2ª basta multiplicar por 20
Para pasar de la 2ª fila a la 1ª dividimos por 20
|
Observa que
|
Las magnitudes número de sacos y peso en kg son directamente proporcionales.
La constante de proporcionalidad para pasar de número de sacos a kg es 20.
Esta manera de funcionar de las proporciones nos permite adentrarnos en lo que llamaremos Regla de tres y que nos servirá para resolver un gran cantidad de problemas matemático.
REGLA DE TRES SIMPLE DIRECTA
Ejemplo 1
En 50 litros de agua de mar hay 1.300 gramos de sal. ¿Cuántos litros de agua de mar contendrán 5.200 gramos de sal?
Como en doble cantidad de agua de mar habrá doble cantidad de sal; en triple, triple, etc. Las magnitudes cantidad de agua y cantidad de sal son directamente proporcionales.
Si representamos por x el número de litros que contendrá 5200 gramos de sal, y formamos la siguiente tabla:
|
Litros de agua |
50 |
x |
|
Gramos de sal |
1.300 |
5.200 |
|
Se verifica la proporción:
|
Y como en toda proporción el producto de medios es igual al producto de extremos (en palabras simples, se multiplican los números en forma cruzada) resulta:
50 por 5.200 = 1.300 por x
|
Es decir
|
En la práctica esto se suele disponer del siguiente modo:
![]()
|
Esta forma de plantear y resolver problemas sobre proporciones se conoce con el nombre de regla de tres simple directa. |
El pocentaje nos dice qué parte de un total representa una cantidad. Y lo hace representando el total por el valor 100 y calculando de esos 100 cuanto correspondería a la cantidad que estamos analizando.
Por ejemplo:
Si hay 10 coches aparcados y 3 son de colo amarillo, ¿Qué porcentaje (que parte del total) representan estos 3 coches?
El total (los 10 coches aparcados) se considera que es el 100 por cien (se representa por 100 %).
Para calcular el porcentaje que representan los 3 coches amarillos:
Se divide el número de cohes amarillos entre el total de coches y se multiplica por 100 (para expresarlo en porcentaje):
3 : 10 = 0,3
0,3 x 100 = 30 %
Los 3 coches amarillos representan el 30% de los coches aparcados.
Para aumentar o disminuir una cantidad en un porcentaje se calcula cuanto representa dicho porcentaje de esa cantidad y se le suma o resta a la cantidad inicial.
Por ejemplo: aumentar 60 en un 20%.
1.- Calculamos cuanto representa el 20%:
(60 x 20) / 100 = 12
2.- Se lo sumamos al importe inicial:
60 + 12 = 72
Veamos otros ejemplos:
Disminuir 50 en un 10%.
1.- Calculamos cuanto representa el 10%:
(50 x 10) / 100 = 5
2.- Se lo restamos al importe inicial:
50 - 5 = 45
Aumentar 120 en un 30%.
1.- Calculamos cuanto representa el 30%:
(120 x 30) / 100 = 36
2.- Se lo restamos al importe inicial:
120 + 36 = 156
Porcentajes (%)
Cuando dices "por ciento" en realidad dices "por cada 100"
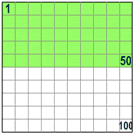 |
Así que 50% quiere decir 50 por 100 (50% de la caja es verde) |
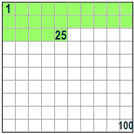 |
| Y 25% quiere decir 25 por 100 (25% de la caja es verde) |
Ejemplos: Porcentajes de 80
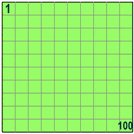 |
100% of 80 is 100/100 × 80 = 80 So 100% means all. |
 |
50% of 80 is 50/100 × 80 = 40 So 50% means half.
|
 |
5% of 80 is 5/100 × 80 = 4 So 5% means 5/100ths. |
Funciones Matemáticas: |
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado codominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito).
En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.
Las funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el costo de una llamada telefónica que depende de su duración, o el costo de enviar una encomienda que depende de su peso.
A modo de ejemplo, ¿cuál sería la regla que relaciona los números de la derecha con los de la izquierda en la siguiente lista?:
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
Los números de la derecha son los cuadrados de los de la izquierda.
La regla es entonces "elevar al cuadrado":
1 --------> 1
2 --------> 4
3 --------> 9
4 --------> 16
x --------> x2.
Para referirse a esta regla podemos usar un nombre, que por lo general es la letra f (de función). Entonces, f es la regla "elevar al cuadrado el número".
Usualmente se emplean dos notaciones:
x --------> x2 o f(x) = x2 .
Así, f(3) significa aplicar la regla f a 3. Al hacerlo resulta 32 = 9.
Entonces f(3) = 9. De igual modo f(2) = 4, f(4) = 16, f(a) = a2, etc.
Veamos algunos ejemplos que constituyen funciones matemáticas.
Ejemplo 1
Correspondencia entre las personas que trabajan en una oficina y su peso expresado en kilos
|
Conjunto X |
Conjunto Y |
|
Ángela |
55 |
|
Pedro |
88 |
|
Manuel |
62 |
|
Adrián |
88 |
|
Roberto |
90 |
Cada persona (perteneciente al conjunto X o dominio) constituye lo que se llama la entrada o variable independiente. Cada peso (perteneciente al conjunto Y o codominio) constituye lo que se llama la salida o variable dependiente. Notemos que una misma persona no puede tener dos pesos distintos. Notemos también que es posible que dos personas diferentes tengan el mismo peso.
Ejemplo 2
Correspondencia entre el conjunto de los números reales (variable independiente) y el mismo conjunto (variable dependiente), definida por la regla "doble del número más 3".
x -------> 2x + 3 o bien f(x) = 2x + 3
Algunos pares de números que se corresponden por medio de esta regla son:
|
Conjunto X |
Conjunto Y |
Desarrollo |
|
− 2 |
− 1 |
f(−2) = 2(−2) + 3 = −4 + 3 = − 1 |
|
− 1 |
1 |
f(−1) = 2(−1) + 3 = −2 + 3 = 1 |
|
0 |
3 |
f(0) = 2(0) + 3 = 0 + 3 = 3 |
|
1 |
5 |
f(1) = 2(1) + 3 = 2 + 3 = 5 |
|
2 |
7 |
f(2) = 2(2) + 3 = 4 + 3 = 7 |
|
3 |
9 |
f(3) = 2(3) + 3 = 6 + 3 = 9 |
|
4 |
11 |
f(4) = 2(4) + 3 = 8 + 3 = 11 |
Con estos ejemplos vamos entendiendo la noción de función: como vemos, todos y cada uno de los elementos del primer conjunto (X) están asociados a uno, y sólo a uno, del segundo conjunto (Y). Todos y cada uno significa que no puede quedar un elemento en X sin su correspondiente elemento en Y. A uno y sólo a uno significa que a un mismo elemento en X no le pueden corresponder dos elementos distintos en Y.
Ahora podemos enunciar una definición más formal:
Una función (f) es una regla que asigna a cada elemento x de un conjunto X (dominio) exactamente un elemento, llamado f(x), de un conjunto Y (codominio).
Otra definición equivalente es: sean X e Y dos conjuntos. Una función de X en Y es una regla (o un método) que asigna un (y sólo uno) elemento en Y a cada elemento en X.
Usualmente X e Y son conjuntos de números.
Generalizando, si se tiene una función f, definida de un conjunto A en un conjunto B, se anota
f : A -----> B (o, usando X por A e Y por B f : X -----> Y) o f(x) = x
Recordemos de nuevo que el primer conjunto A se conoce como dominio (Dom) de la función y B es el codominio o conjunto de llegada.
f(x) denota la imagen de x bajo f, mientras que x es la preimagen de f(x).
En el ejemplo 2 anterior el número 3 es la imagen del número 0 bajo f; por su parte, 1 es la preimagen del número 5.
El rango (Rg) o recorrido (Rec) o ámbito (A) es el conjunto de todos los valores posibles de f(x) que se obtienen cuando x varía en todo el dominio de la función.
Ejemplo 3
Suponga que el conjunto A (de salida) es A = {1, 2, 3} y que el conjunto B (de llegada) es B = {0, 4, 6, 8, 10, 12} y que la relación de dependencia o correspondencia entre A y B es "asignar a cada elemento su cuádruplo".
Vamos a examinar si esta relación es una función de A en B y determinaremos dominio y recorrido.
Veamos:
A los elementos 1, 2 y 3 del conjunto A les corresponden, respectivamente, los elementos 4, 8 y 12 del conjunto B. Como a cada elemento de A le corresponde un único elemento de Y, la relación de dependencia es una función (función de A en B).
Dominio = {1, 2, 3} Recorrido = {4, 8, 12}
Notar que el recorrido es un subconjunto del codominio B = {0, 4, 6, 8, 10, 12}
Aquí debemos recordar que toda función es una relación, pero no todas las relaciones son funciones. Como ejemplos de relaciones que son funciones y algunas que no lo son, veamos las siguientes:
Si tenemos los conjuntos
A = {1; 2; 3; 4}, B = {1; 2; 3; 4; 5}
Podemos establecer las relaciones
f = { (1; 2); (2; 3); (3; 4); (4; 5) }
g = { (1; 2); (1; 3); (2; 4); (3; 5); (4; 5) }
h = { (1; 1); (2; 2); (3; 3) }:
Está claro que f, g y h son relaciones de A en B, pero sólo f es una función (todos los elementos del conjunto A tiene su correspondiente elemento en b); g no es función ya que (1; 2) y (1; 3) repiten un elemento del dominio (el 1). Tampoco h es una función ya que Dom(h) = {1; 2; 3} ≠ A (falta el 4).
Ejemplo 4
Sea X = {−4, −1, 0, 4, 9}, Y = {−4,−3, −2, −1, 0, 1, 2, 3, 4} y que la regla de correspondencia es " asignar a cada elemento de X el resultado de extraer su raíz cuadrada".
Vamos a determinar si esta regla constituye función de X en Y.
Veamos:
A simple vista se aprecia que los números 0, 4, 9 tienen imagen en Y (![]() ), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.
), pero a los números −4 y −1 no les corresponden elementos en Y. Como existen elementos de X que no se corresponden con elementos de Y, esta relación no es función de X en Y.
Dominio y rango de una función
Como ya vimos, el dominio de una función es el conjunto de valores para los cuales la función está definida; es decir, son todos los valores que puede tomar la variable independiente (la x).
Por ejemplo la función f(x) = 3x2 – 5x está definida para todo número real (x puede ser cualquier número real). Así el dominio de esta función es el conjunto de todos los números reales.
En cambio, la función ![]() tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
tiene como dominio todos los valores de x para los cuales −1< x < 2, porque aunque pueda tomar cualquier valor real diferente de –2, en su definición determina en qué intervalo está comprendida.
Si el dominio no se específica, debe entenderse que el dominio incluye a todos los números reales para los cuales la función tiene sentido.
En el caso de la función ![]() , el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
, el dominio de esta función son todos los números reales mayores o iguales a –3, ya que x + 3 debe ser mayor o igual que cero para que exista la raíz cuadrada.
Como resumen, para determinar el dominio de una función, debemos considerar lo siguiente:
Si la función tiene radicales de índice par, el dominio está conformado por todos los números reales para los cuales la cantidad subradical sea mayor o igual a cero.
Si la función es un polinomio; una función de la forma f(x) = a0 + a1x + a2x2 +...+ anxn (donde a0, a1, a2,..., an son constantes y n un entero no negativo), el dominio está conformado por el conjunto de todos los números reales.
Si la función es racional; esto es, si es el cociente de dos polinomios, el dominio está conformado por todos los números reales para los cuales el denominador sea diferente de cero.
El rango (recorrido o ámbito) es el conjunto formado por todas las imágenes; es decir, es el conjunto conformado por todos los valores que puede tomar la variable dependiente; estos valores están determinados además, por el dominio de la función.
Ejemplo
Identificar dominio y rango de la función ![]()
Veamos:
Como la función tiene radicales el dominio está conformado por todos los valores para los cuales x – 2 ≥ 0. Esto es, el dominio de la función incluye todos los reales que son mayores o iguales a 2.
El rango es igual al conjunto de los números reales positivos incluyendo el cero; puesto que al reemplazar los valores del dominio se obtienen únicamente valores positivos bajo la función f.
Tipos de Función |
Intuitivamente, la palabra función se refiere a una correspondencia de un conjunto con otro. Por ejemplo:
Considera un conjunto de estudiantes (X) y un conjunto de edades (Y), en que a cada estudiante le
corresponde un número que es su edad en años.
|
Estudiante (Conjunto X) |
Edad (Conjunto Y) |
|
José |
19 |
|
María |
18 |
|
Manuel |
21 |
|
Soledad |
18 |
|
Alberto |
20 |
En la tabla se observa que a cada estudiante le corresponde una edad. A ese tipo de asociación se le
llama función.
Recordemos la definición:
En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro
conjunto de elementos Y (llamado codominio de forma que a cada elemento x del dominio le corresponde
un único elemento f(x) del codominio (los que forman el recorrido, rango o ámbito).
De manera más simple: Una función es una relación entre dos magnitudes, de tal manera que a cada
valor de la primera corresponde un único
valor de la segunda.
En el ejemplo anterior el dominio es {José, María, Manuel, Soledad, Alberto} y el recorrido es
{18, 19, 20, 21}.
La función se puede ilustrar mediante un diagrama usando flechas para indicar la forma en que se
asocian los elementos de los dos conjuntos.
Nota: Si x es un elemento en el dominio de la función, entonces el elemento en el recorrido que
f asocia con x se denota simbólicamente f(x),
y se llama la imagen de x bajo la función f. En el ejemplo anterior f(Soledad) = 18, f(Manuel) = 21.
También se conoce la imagen como el
valor de la función f en x.
Básicamente, hay tres formas para expresar una función: mediante una tabla de valores
(como el ejemplo anterior), mediante una
expresión algebraica o, como veremos luego, mediante una gráfica.
Tipos de funciones
Dependiendo de ciertas características que tome la expresión algebraica o notación de
la función f en x, tendremos distintos
tipos de funciones:
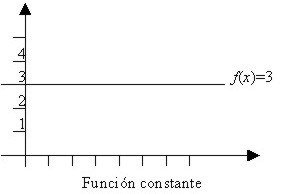
Función constante
Una función de la forma f(x) = b, donde b es una constante, se conoce como una función constante.
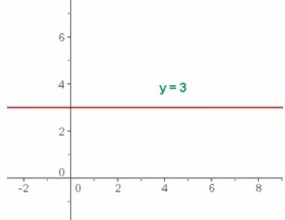
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde el dominio es el conjunto de los números reales
y el recorrido es {3},
por tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
 |
 |
Función lineal
Una función de la forma f(x) = mx + b se conoce como una función lineal, donde m representa la pendiente y b
representa el intercepto en y. La representación gráfica de una función lineal es una recta. Las funciones lineales
son funciones polinómicas.
Ejemplo:
f(x) = 2x − 1
es una función lineal con pendiente m = 2 e intercepto en y en (0, −1). Su gráfica es una recta ascendente.
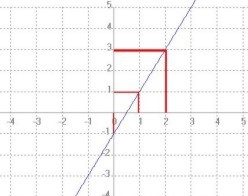 |
| f(x) = 2x − 1 |
En general, una función lineal es de la forma
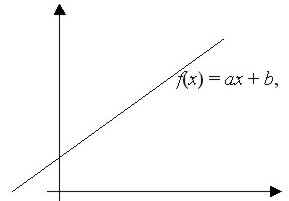 |
| f(x) = ax + b, donde a y b son constantes (la a es lo mismo que la m anterior (corresponde a la pendiente). |
Para trazar la gráfica de una función lineal solo es necesario conocer dos de sus puntos.
La ecuación matemática que representa a esta función, como ya vimos, es f(x) = ax + b, donde f(x) corresponde al valor de y,
entonces
y = ax + b
Donde “a” es la pendiente de la recta, y “b” es la ordenada al origen.
La pendiente indica la inclinación de la recta, cuanto sube o baja y cuanto avanza o retrocede. Esto depende del signo que tenga.
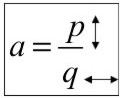
El valor de “a” siempre es una fracción (si no tiene nada abajo, es porque tiene un 1), donde el numerador (p) me indica cuanto sube o
baja, y el denominador (q) indica cuanto avanzo o retrocedo.
Aprendido esto, y según el signo de la fracción, la pendiente se marca de la siguiente forma
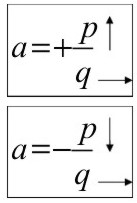
La ordenada al origen (b) es el valor donde la recta corta al eje y.
La recta siempre va a pasar por el punto (0; b)
Representación gráfica de una función lineal o función afín
Para graficar una recta, alcanza con los datos que da la ecuación matemática de la función, y se opera de la siguiente manera:
1. Se marca sobre el eje y la ordenada al origen, el punto por donde la recta va a cortar dicho eje.
2. Desde ese punto, subo o bajo según sea el valor de “p” y avanzo o retrocedo según indique el valor de “q”. En ese nuevo lugar, marco
el segundo punto de la recta.
3. Se podría seguir marcando puntos con la misma pendiente, pero con 2 de ellos ya es suficiente como para poder graficar la recta.
4. Teniendo ya los dos puntos, con regla se traza la recta que pasa por los mismos.
Ejemplo:
Graficar la siguiente función:
![]()
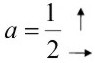
La ordenada al origen (3) me indica que me debo parar sobre el eje y en el 3.
De ahí subo 1 y avanzo 2, como me lo indica la pendiente.
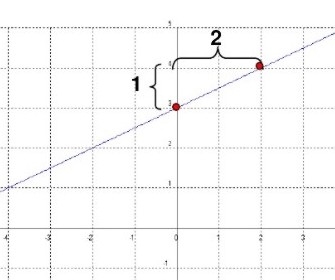 |
También podemos graficar una función dando valores a x y obteniendo dos puntos en las coordenadas.
Ejemplo
Graficar la función dada por f(x) = 2x – 1
Solución
Como la función es lineal se buscan dos puntos de la recta; para ello, se le dan valores a x y se encuentran sus imágenes
respectivas, esto es:
Si x = 0, se tiene que f(0) = 2(0) – 1 = − 1
Si x = 2, se tiene que f(2) = 2(2) – 1 = 3
Así, los puntos obtenidos son (0, −1) y (2, 3), por los cuales se traza la gráfica correspondiente.
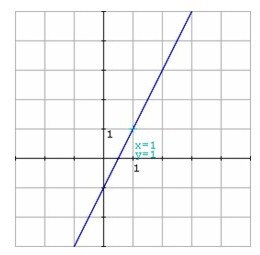 |
Veamos ahora el proceso inverso; o sea, si tenemos la gráfica de una función queremos encontrar su expresión analítica
o matemática.
Para eso, necesitamos encontrar una expresión de la forma f(x) = ax + b a partir de la gráfica.
Por ejemplo, a partir de la siguiente gráfica, vamos a calcular su expresión matemática.
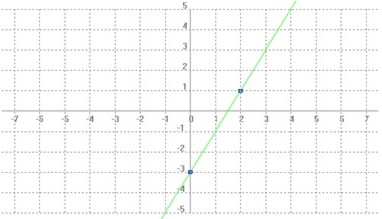 |
La imagen de 0 es b porque f(0) = a(0) + b = b luego b = –3
Tomamos otro punto, por ejemplo, el (2, 1); el 1 es la imagen del 2 luego se cumple que:
1 = a(2) + b → 1 = 2a – 3 → 4 = 2a → a = 2
Nuestra recta será: f(x) = 2x – 3
Función polinómica
Una función f es una función polinómica si,f(x) = anxn + an−1xn−1 + ... + a1x + a0
donde a0, a1,...,an son números reales y los exponentes son enteros positivos.
Ejemplos:
f(x) = x2 − 2x − 3;
g(x) = 5x + 1;
h(x) = x3
El dominio de todas estas funciones polinómicas es el conjunto de los números reales (porque el elemento x puede ser cualquier número real).
Función cuadrática
Una función de la forma f(x) = ax2 + bx + c, donde a, b y c son constantes y a es diferente de cero, se conoce como una función cuadrática.
La representación gráfica de una función cuadrática es una parábola. Una parábola abre hacia arriba si a > 0 y abre hacia abajo si a < 0.
El vértice de una parábola se determina por la fórmula:
![]()
Las funciones cuadráticas son funciones polinómicas.
Ejemplo:
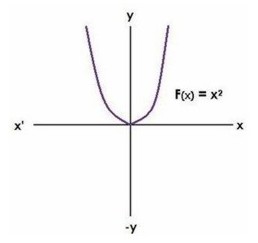 |
| f(x) = x2 representa una parábola que abre hacia arriba con vértice en (0,0). |
Función racional
Una función racional es el cociente de dos funciones polinómicas. Así es que q es una función racional si para todo x en el dominio,
se tiene:
![]()
para los polinomios f(x) y g(x).
Ejemplos:
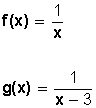
Nota: El dominio de una función polinómica son los números reales; sin embargo, el dominio de una función racional consiste
de todos los números reales excepto los ceros del polinomio en el denominador (ya que la división por cero no está definida).
Función de potencia
Una función de potencia es toda función de la forma f(x) = xr, donde r es cualquier número real.
Las funciones f(x) = x4/3 y h(x) = 5x3/2 son funciones de potencia
Ejercicios y ejemplos con funciones en general:
Expresar mediante una fórmula la función que asocia a cada número:
a) Su cuádruplo.
La función es: f (x) = 4x.
b) Un número 2 unidades mayor.
La función es: f (x) = x + 2.
c) Su mitad menos 1.
La función es: f (x) = x/2 − 1.
d) El cuadrado del número que es una unidad menor.
La función es: f (x) = (x − 1)2
Veamos algunos otros ejemplos de funciones:
1) El volumen de un gas está determinado por la presión (a temperatura constante), esta relación viene dada por la ley de Boyle-Mariotte:
![]()
donde v representa el volumen del gas en litros, p es la presión en atmósferas y c es una constante de proporcionalidad.
Se observa que al variar la presión a la que está sometido el gas varía el volumen; es decir, los valores del volumen dependen de los valores
de la presión del gas y para cada valor de la presión existe un único valor del volumen.
2) El área A del círculo depende de la longitud de su radio r y está dada por la fórmula:
![]()
Si se conoce el valor del radio se puede conocer el valor del área del círculo.
3) Dada la función f(x) = 5x2 + 2
Encontrar el valor de la función para cuando x = 2.
Para calcular la imagen de un elemento bajo la función f, se reemplaza dicho elemento en el lugar de la variable, así para x = 2
f(2) = 5(2)2 + 2
f(2) = 22
por lo tanto cuando x = 2, se tiene que f(2) = 22.
Un problema resuelto
El precio de arrendar un auto es de 15 dólares más 0,20 de dólar por kilómetro recorrido.
a) Hallar la fórmula que expresa el costo del arriendo en función del número de los kilómetros recorridos.
b) ¿Cuánto hay que pagar si se han recorrido 50 kilómetros?
c) Si han cobrado 53 dólares ¿cuántos kilómetros se han recorrido?
Veamos:
a) Si llamamos x al número de kms recorridos, la fórmula de la función es f (x) = 15 + 0,2x.
b) x = 50 entonces
f (50) = 15 + 0,2 • 50 = 25
Hay que pagar 25 dólares.
c) f (x) = 53 entonces
15 + 0,2x = 53 entonces x = 190
Se han recorrido 190 km.
Álgebra de funciones
Suma, resta, multiplicación y división de funciones
Sean f y g dos funciones cualesquiera.
Se define ![]() como
como
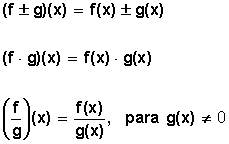
Ejemplos:
Suma de funciones
Sean las funciones
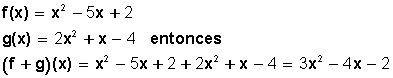
Resta de funciones
![]()
Producto de funciones
Sean las funciones
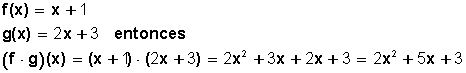
División de funciones
Sean las funciones
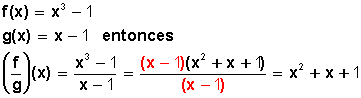
Nótese que hemos factorizado por (x − 1)
Ejemplo para practicar:
Sean f(x) = 3x3 + 7 y g(x) = x2 – 1. Hallar la suma, diferencia, producto y cociente de las funciones.
Fracciones algebraicas |
Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.
Son fracciones algebraicas:
![]()
Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.
El valor de una fracción no se altera si se multiplican o dividen el numerador y denominador por una misma cantidad. Esta cantidad debe ser distinta de cero.
Por ejemplo:
Si ![]() se multiplica por x + 2 en su numerador y denominador resulta:
se multiplica por x + 2 en su numerador y denominador resulta:
![]()
Se recomienda hacer las operaciones con calma y mucha concentración ya que son frecuentes los errores de signos y los errores en el uso incorrecto de paréntesis.
Operaciones con fracciones algebraicas
Simplificar fracciones algebraicas
La simplificación de fracciones algebraicas es objeto de frecuentes errores, pero se simplifican igual que las fracciones ordinarias: dividiendo el numerador y el denominador por factores comunes. Entonces, la clave está en el factor común. Para simplificar al máximo habrá que factorizar los polinomios numerador y denominador.
Por ejemplo, simplificar:
![]()
Otro ejemplo, simplificar la fracción
![]()
Primero, factorizamos los polinomios del numerador y del denominador, para quedar
![]()
Como vemos, simplificar (o reducir) una fracción algebraica consiste en transformarla a otra equivalente cuya particularidad es ser irreductible (se puede simplificar sólo hasta un cierto nivel).
Suma y resta de fracciones algebraicas
Para sumar y restar procederemos de forma similar a como lo hacemos con fracciones de números enteros, reduciendo primero a común denominador.
Igual como ocurre con las fracciones de números enteros, la suma y resta de fracciones algebraicas puede ser con fracciones de igual denominador o de distinto denominador.
Suma y resta de fracciones algebraicas con igual denominador
Veamos el siguiente ejemplo de suma y resta:
![]()
Como el denominador es común (x + 1), este se ha unificado en una sola fracción, que ahora tiene como numerador a todas las cantidades que eran numeradores en las fracciones que estamos sumando y restando. Nótese que dichas cantidades se anotan entre paréntesis cuando no son monomios, para no confundir luego los signos.
Ahora sacamos los paréntesis teniendo cuidado de cambiar el signo interior cuando delante del paréntesis hay un signo menos (−), y nos queda
![]()
Hicimos las operaciones posibles y llegamos al resultado.
Suma y resta de fracciones algebraicas con distinto denominador
Veamos el siguiente ejemplo:
![]()
Tal como lo hacíamos al sumar o restar fracciones de números enteros, utilizando el mínimo común múltiplo (m.c.m.) las fracciones con distintos denominadores se transforman en fracciones equivalentes con denominador común.
Entonces, que debemos hacer: encontrar el m.c.m. de los denominadores, que llamaremos mínimo común denominador (m.c.d.).
Para calcular el m.c.m. factorizamos
| 5ab | a2 | 15b2 | a | |
| 5b | a | 15b2 | a | |
| 5b | 1 | 15b2 | b | |
| 5 | 1 | 15b | b | |
| 5 | 1 | 15 | 5 | |
| 1 | 1 | 3 | 3 | |
| 1 | 1 | 1 |
Multiplicamos los factores y queda a • a • b • b • 5 • 3 = a2 • b2 • 15 que es lo mismo que 15a2b2 y es el mínimo común denominador (m.c.d.) de las tres fracciones involucradas.
Conocido el m.c.d. operamos con fracciones con denominador común:
Previamente, dividimos el denominador común (15a2b2) por cada uno de los denominadores individuales, para conocer la cifra o valor que se multiplica por cada uno de los numeradores, y lo hacemos así:
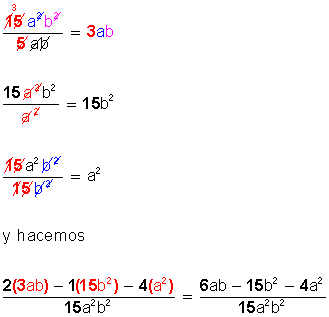
Esta es la forma tradicional de operar cuando hemos hallado el m.c.d. Pero también hay otra, como la siguiente:
Encontrado el m.c.d. (15a2b2) se multiplica cada fracción (tanto numerador como denominador) por los términos que faltan por completar dicho m.c.d., del modo siguiente:
![]()
Nótese que “los términos que faltan” se obtienen haciendo la misma división del caso anterior.
Un ejemplo más:
Sumar ![]()
El m.c.m. de los denominadores, o mínimo común denominador (m.c.d.) es x(x − 3)
Hacemos
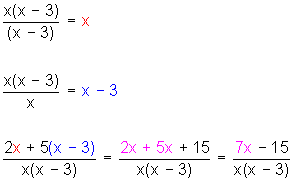
¿Qué hicimos? Sumamos los numeradores dejando el mismo denominador y simplificamos el numerador:
Producto (multiplicación) de fracciones algebraicas
Para multiplicar fracciones algebraicas procederemos igual como lo hacemos con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Veamos qué significa esto:
Sea ![]() una fracción algebraica cualquiera que está multiplicada por otra
una fracción algebraica cualquiera que está multiplicada por otra ![]() , entonces:
, entonces: ![]()
Veamos ahora ejemplos de multiplicación (producto) de fracciones algebraicas
Multiplicar
![]()
Anotamos la multiplicación de los numeradores y de los denominadores:
![]()
Simplificamos antes de efectuar el producto:
![]()
Ahora, podemos multiplicar los factores finales:
![]()
Ejemplos desarrollados
a) ![]()
b) ![]()
c)![]()
Importante: en los tres ejemplos anteriores (como en casi todos los casos) es preciso dominar la factorización de productos notables.
Cociente o división de fracciones algebraicas
Para dividir fracciones algebraicas procederemos igual como lo hacemos con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Veamos, ahora qué significa esto:
Sea ![]() una fracción algebraica cualquiera que está dividida por otra
una fracción algebraica cualquiera que está dividida por otra ![]() , entonces:
, entonces:
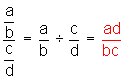
Veamos ahora ejemplos de división (cociente) de fracciones algebraicas
Dividir
![]()
Anotamos haciendo el producto cruzado:
![]()
Simplificamos y finalmente multiplicamos:
![]()
Potencias |
Una potencia es un producto de factores iguales. Está formada por la base y el exponente.
| Exponente |
Se puede leer: tres elevado a cuatro o bien tres elevado a la cuarta |
|
| 3 . 3 . 3 . 3 = 34 | ||
| Base |
El factor que se repite se llama base. El número de veces que se repite el factor, o sea la base, se llama exponente. Esto significa que si se tiene la potencia 2 6 (dos elevado a seis o a la sexta), la base será 2 y el exponente 6, lo cual dará como resultado 64 porque el 2 se multiplica por si mismo 6 veces (2 · 2 · 2 · 2 · 2 · 2 = 64).
Ejemplos:
2 5 = 2 • 2 • 2 • 2 • 2 = 32 El exponente es 5, esto significa que la base, el 2, se debe multiplicar por sí misma cinco veces.
3 2 = 3 • 3 = 9 El exponente es 2, esto significa que la base (3) se debe multiplicar por sí misma dos veces.
5 4 = 5 • 5 • 5 • 5 = 625 El exponente es 4, esto significa que la base (5) se debe multiplicar por sí misma cuatro veces.
Una potencia puede representarse en forma general como:
| an = a • a • a • ........ |
Donde: a = base n = exponente “ n” factores iguales
Finalmente, recuerda que una de las aplicaciones de las potencias es la descomposición factorial de un número.
Potencia de base entera y exponente natural
Si la base a pertenece al conjunto de los Nuemeros enteros ( a ![]() Z ) (léase a pertenece a zeta) significa que puede tomar valores positivos y negativos. Si el exponente pertenece al conjunto de los numeros naturales, significa que puede tomar valores del uno en adelante (1, 2, 3, .....).
Z ) (léase a pertenece a zeta) significa que puede tomar valores positivos y negativos. Si el exponente pertenece al conjunto de los numeros naturales, significa que puede tomar valores del uno en adelante (1, 2, 3, .....).
Potencia de base entera positiva:
Si la base a es positiva, la potencia siempre será un entero positivo, independiente de los valores que tome el exponente, es decir, de que sea par o impar.
| (+a) n = +a n |
Ejemplos:
(+4) 3 = 43 = 4 • 4 • 4 = 64 = + 64 Exponente impar
(+3) 4 = 34 = 3 • 3 • 3 • 3 = 81 = +81 Exponente par
Potencia de base entera negativa:
Si la base a es negativa el signo de la potencia dependerá de si el exponente es par o impar.
a) Si el exponente es par, la potencia es positiva.
| (_ a) n (par) = +a n |
Ejemplos:
(_5) 2 = _5 • _5 = +25 = 25 _ · _ = +
(_2) 8 = _2 • _2 • _2 • _2 • _2 • _2 • _2 • _2 = +256 = 256
b) Si el exponente es impar, la potencia es negativa.
| (_a) n (impar) = _a n |
Ejemplos:
(_2) 3 = _2 • _2 • _2 = _8
(_3) 3 = _3 • _3 • _3 = _27
En resumen:
|
Base |
Exponente |
Potencia |
|
Positiva |
Par |
Positiva |
|
Positiva |
Impar |
Positiva |
|
Negativa |
Par |
Positiva |
|
Negativa |
Impar |
Negativa |
Multiplicación de potencias de igual base
Para multiplicar potencias de igual base, se suman los exponentes y se mantiene la base.
|
|
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
División de potencias de igual base
Para dividir potencias de igual base, se restan los exponentes y se conserva la base.
|
|
Ejemplos:
1) ![]()
2)![]()
3)![]()
Multiplicación de potencias de igual exponente
Se multiplican las bases y se conserva el exponente.
Ejemplo:
![]()
División de potencias de igual exponente
Se dividen las bases y se conserva el exponente
Ejemplo:
![]()
Potencia elevada a potencia
Se eleva la base al producto (multiplicación) de los exponentes; o sea, se conserva la base y se multiplican los exponentes.
|
|
Ejemplos:
1) ![]()
2) ![]()
Potencia de base racional y exponente entero
Sea la base ![]() (fracción) perteneciente al conjunto de los Números Racionales (
(fracción) perteneciente al conjunto de los Números Racionales (![]()
![]() Q ), donde a es el numerador y b el denominador distinto de cero, y el exponente pertenece a los números enteros (n
Q ), donde a es el numerador y b el denominador distinto de cero, y el exponente pertenece a los números enteros (n ![]() Z). Para elevar una fracción a potencia se elevan por separado numerador y denominador.
Z). Para elevar una fracción a potencia se elevan por separado numerador y denominador.
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
Potencia de exponente negativo
Si ![]() es un número racional y – n un número entero, entonces se tiene,
es un número racional y – n un número entero, entonces se tiene,
| Si el exponente es negativo el numerador se invierte con el denominador, y el exponente cambia de signo. |
Ejemplos:
1) ![]()
2) ![]()
3) ![]()
El lenguaje algebraico |
El lenguaje que usamos en operaciones aritméticas en las que sólo intervienen números se llama lenguaje numérico.
En ocasiones empleamos letras para representar cualquier número desconocido, realizamos operaciones aritméticas con ellas e, incluso, las incluimos en expresiones matemáticas para poder calcular su valor numérico.
El lenguaje que utiliza letras en combinación con números y signos, y, además, las trata como números en operaciones y propiedades, se llama lenguaje algebraico.
La parte de las Matemáticas que estudia la relación entre números, letras y signos se llama Álgebra.
Características del lenguaje algebraico
1.- El lenguaje algebraico es más preciso que el lenguaje numérico: podemos expresar enunciados de una forma más breve.
El conjunto de los múltiplos de 5 es 5 • = {±5, ±10, ±15, ...}.
En lenguaje algebraico se expresa 5 • n, con n un número entero.
2.- El lenguaje algebraico permite expresar relaciones y propiedades numéricas de carácter general.
La propiedad conmutativa del producto se expresa a • b = b • a, donde a y b son dos números cualesquiera.
3.- Con el lenguaje algebraico expresamos números desconocidos y realizamos operaciones aritméticas con ellos.
El doble de un número es seis se expresa 2 • x = 6.
Expresiones algebraicas
Una expresión algebraica es un conjunto de números y letras que se combinan con los signos de las operaciones aritméticas. Una expresión algebraica se define como aquella que está constituida por coeficientes, exponentes y bases.
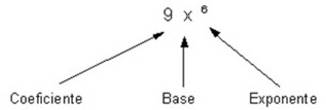
Coeficiente numérico: es la cantidad numérica o letra que se encuentra a la izquierda de la base, la cual indica la cantidad de veces que la base se debe sumar o restar dependiendo del signo que tenga.
Ejemplos:
7x4 = x4 + x4 + x4 + x4 + x4 + x4 + x4
– 3x2 = – x2 – x2 – x2
Exponente numérico: es la cantidad que se encuentra arriba a la derecha de la base, la cual indica la cantidad de veces que la base se toma como producto.
Ejemplos:
5x3 = 5 (x) (x) (x)
8( – x + 5)2 = 8(– x + 5) (– x + 5)
Valor numérico de una expresión algebraica
El valor numérico de una expresión algebraica es el número que resulta de sustituir las letras por números y realizar a continuación las operaciones que se indican.
Una cantidad desconocida se puede representar con alguna letra llamada variable.

PORQUE NO LE ENTIENDO A LAS MATEMATICAS
Muchas veces los verdaderos problemas en matemáticas que tenemos son de técnicas de estudio y no de dificultades con los números. Se ha demostrado cientificamente que las personas con discalculia, que es un problema genético, Es decir que tienen problemas en matemáticas, el resto de la humanidad, lo que tiene son problemas con sus técnicas de estudio, es decir, con su manera de estudiar muchas veces estudiamos matematicas como cuando estudiamos para un examen de ciencias sociales.
Enfocarse en un tema, es una de las técnicas de estudio fundamentales para terminar con tus problemas en matemáticas. A través de pruebas científicas se ha demostrado que cuando pierdes la concentración, demoras hasta 15 minutos en volver a alcanzar la misma concentración que tenías antes de la interrupción. Si tomamos en cuenta que una de las técnicas de estudio correctas es no dedicar más de una hora seguida a una actividad, podemos decir entonces que una sola interrupción ¡baja tu rendimiento en un 25%!, si durante tu estudio sufres más de una interrupción… ¡es obvio el motivo por el cual tienes problemas en matemáticas!
ESTRATEGIAS PARA APRENDER MATEMATICAS

Lo peor que podemos decir es "No me gustan las matemáticas o simplemente no he nacido para esto y como definitivo las matemáticas son muy difíciles yo no pienso estudiar algo que lleve matemáticas, que estudien los que quieren ser ingenieros o de plano, para qué me sirve este curso con que llegue a estudiar para licenciado con eso basta, para no ver números, además me la paso estudiando horas y horas y siempre salgo mal en los exámenes, no entiendo dada del curso, estoy mal en el curso, entiendo lo que me explican y en los exámenes no sé qué hacer, memorizo ejercicios y en el examen se me olvida todo o simplemente decimos es que no se le entiende al profesor , estudio con mis compañeros y no me funciona, no tengo suficiente tiempo para estudiar, recuerdo que hoy mi amigo me invito a jugar Xbox, mi amiga se va a ir a comprar ropa y me pidió que la acompañara, etc."
Si en alguna ocasión ha pasado por tu mente alguna de las ideas mencionadas anteriormente, debes leer esto.
¿En qué momento empieza mi estudio?
1. Mi profesor en el primer día de clase, además de presentarse, nos regaña y nos amenaza que todos van a reprobar, nos es entrega el contenido del curso y posiblemente una referencia bibliográfica donde están los temas que se tocarán durante el ciclo y si no lo hace hay que pedir los contenidos del curso.
2. El profesor entrega los contenidos del curso pero no es para perder tiempo en clases, es más bien para que tú como alumno responsable que eres, o lo serás, los tengas siempre presente y puedas preparar los temas antes de cada clase y una vez en ella puedas comprender mejor y entender lo que él te pueda explicar.
3. En el primer día de clase
Al dia siguiente de clases trata o más bien lee, repasa y si faltaste entérate de lo que se hizo en las clases anteriores y como ya tienes los contenidos del curso y la referencia bibliografica, lo que debes hacer es revisar tu libro, apuntes pasados, separatas, etc., buscando, por lo menos, los temas que tocará el profesor en la próxima clase.
No sólo te dediques a buscar libros, sino también léelos y trata de entenderlos, esto te ayudará a comprender mucho mejor la clase siguiente.
Un Estrategia que realizaba en mis tiempos de estudios era realizar fichas bibliográficas apuntando los títulos de los libros que mejor entiendes, aquellos donde puedas encontrar una explicación clara de la teoría, donde halles más y mejores ejercicios, de esta manera, podrás saber cuáles son básicos y cuáles te ayudarán a profundizar más en el tema, además en ellas puedes organizarlas con apuntes específicos que te pueden ayudar posteriormente, lo que nunca dejes de hacer es preparar tus cosas de clases para que cuando llegue el maestro tengas a la disposición todas tus herramientas necesarias para enfrentar la clase de matemáticas o de física.
4. Tener buenos apuntes.Lo típico llega la revisión de libreta por parte de tu profesor y no tienes nada de apuntes o unos días antes te encuentras desvelándote para pasar los apuntes que además la libreta que te prestaron también se encuentra incompleta y lo peor del caso cuando no sabes o ya no tienes tiempo de pasar la libreta, le dices a tu profesor “ el día de ayer la perdí profe, no la encuentro como me estoy cambiando de casa no se donde la puso mi mama o también que cree profe ayer me asaltaron y se llevaron mi mochila, usted cree profe cuanta gente mala hay, verdad. Es ahí donde tu problema es mas fuerte pues no tienes las herramientas con las que debes de enfrentarte para entender materias de mayor complejidad
Concepto de fracción |
El concepto matemático de fracción corresponde a la idea intuitiva de dividir una totalidad en partes iguales, como cuando hablamos, por ejemplo, de un cuarto de hora, de la mitad de un pastel, o de las dos terceras partes de un depósito de gasolina. Tres cuartos de hora no son, evidentemente, la misma cosa que las tres cuartas partes de un pastel, pero se “calculan” de la misma manera: dividiendo la totalidad (una hora, o el pastel) en cuatro partes iguales y tomando luego tres de esas partes. Por esta razón, en ambos casos, se habla de dividir dicha unidad (una hora, un pastel, etc.) en 4 partes iguales y tomar luego 3 de dichas partes.
Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.
La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.
TÉRMINOS DE UNA FRACCIÓN
| a | Numerador |
| — | - |
| b | Denominador |
El Numerador indica el número de partes iguales que se han tomado o considerado de un entero. El Denominador indica el número de partes iguales en que se ha dividido un entero.
Por ejemplo, la fracción 3 / 4 (se lee tres cuartos) tiene como numerador al 3 y como denominador al 4. El 3 significa que se han considerado 3 partes de un total de 4 partes en que se dividió el entero o el todo.
La fracción 1 / 7 (se lee un séptimo) tiene como numerador al 1 y como denominador al 7. El numerador indica que se ha considerado 1 parte de un total de 7 (el denominador indica que el entero se dividió en 7 partes iguales).
Ejemplos:
| Hay 8 partes de las cuales se han pintado 5, por lo tanto, la fracción que representa matemáticamente este dibujo es 5 / 8 (se lee cinco octavos). | 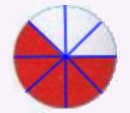 |
|
Hay 3 partes pintadas de un total de 5. Esto se representa como 3 / 5 (se lee tres quintos) |
 |
Debes tener presente que existen distintas posibilidades para representar gráficamente una fracción, es decir, se puede representar con distintos dibujos; lo importante es tener siempre presente el concepto de fracción.
Por ejemplo, la fracción 5 / 8, que ya vimos arriba, está representada a continuación de otras dos formas distintas:
|
Hay 5 partes pintadas de un total de 8 partes. Esto se representa como 5 / 8 (se lee cinco octavos) |
 |
|
Hay 5 partes pintadas de un total de 8 partes. Esto se representa como 5 / 8 (se lee cinco octavos) |
 |
Otros ejemplos:
|
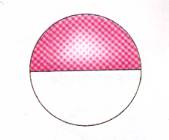
Hay 1 parte pintada de un total de 2 partes. Esto se representa como 1 / 2 (se lee un medio) |
 |
|
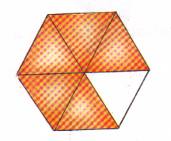
Hay 5 partes pintadas de un total de 6 partes. Esto se representa como 5 / 6 (se lee cinco sextos) |
 |




![TEX: \[<br />\frac{a}<br />{b} = \frac{b}<br />{c}\,\,\,\,\,\,\,\,\,\,o\,\,\,\,\,\,\,\,\,\,\frac{a}<br />{b} = \frac{c}<br />{a}<br />\]<br /> <br />](https://fmat.cl/tex/f2fe868cee8052946c7b31d0606ef4f4.png)